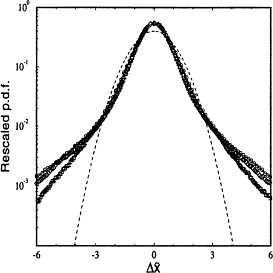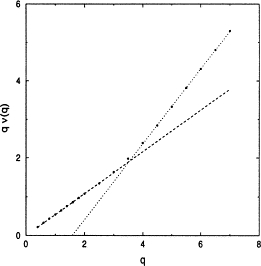
$$ \operatorname{E}|\xi_{t}-\operatorname{E}\xi_{t}|^{q}\propto t^{q\,\nu(q)} $$
In Castiglione et al (1999) we inquired the mechanisms
underlying genuine multiscaling in diffusion processes. Strong anomalous diffusion appears in fine-tuned parametric regions of chaotic dynamical systems.