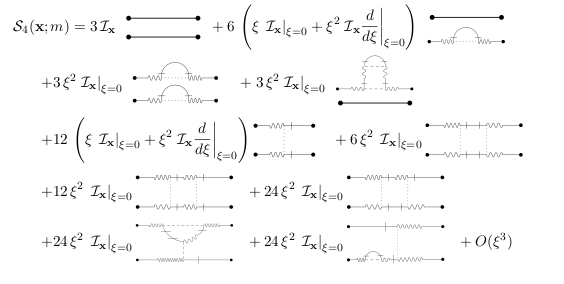
$$ \mathcal{S}_{2\,n}(\boldsymbol{x};m)=\operatorname{E}|\theta(\boldsymbol{x};m)-\theta(\boldsymbol{0};m)|^{2\,n}\propto \|\boldsymbol{x}\|^{\zeta_{2\,n}(\xi)} $$
Kraichnan's model of passive advection is to-date the only PDE model of turbulence where intermittency and multiscaling can be proven in a mathematically controlled fashion. The result was first independently derived in the diffusion , large dimension , and laminar limits and numerically also by us here.