$$ E\,\geq\,\mathrm{K_{B}}\,T\,\ln 2 $$
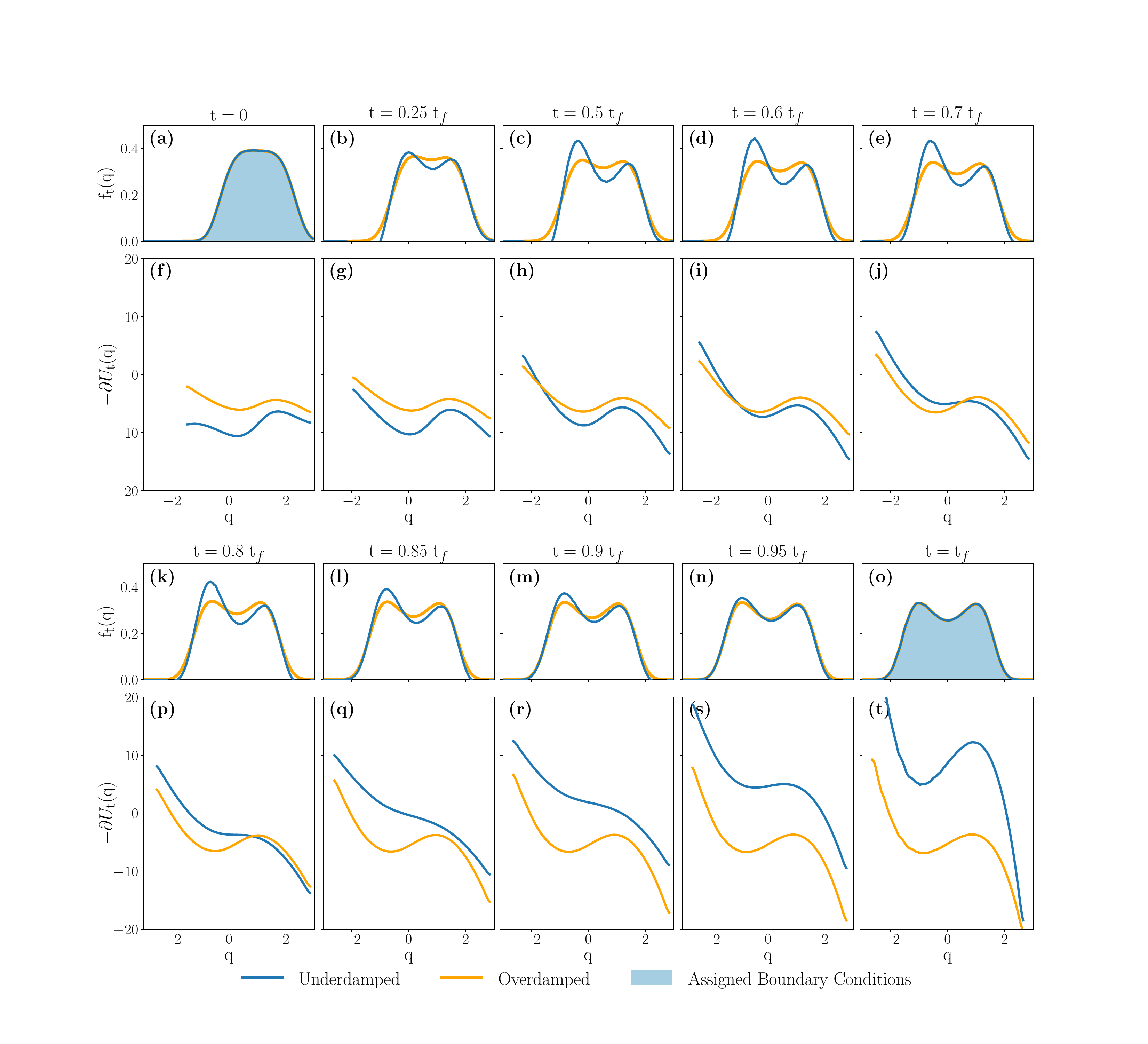
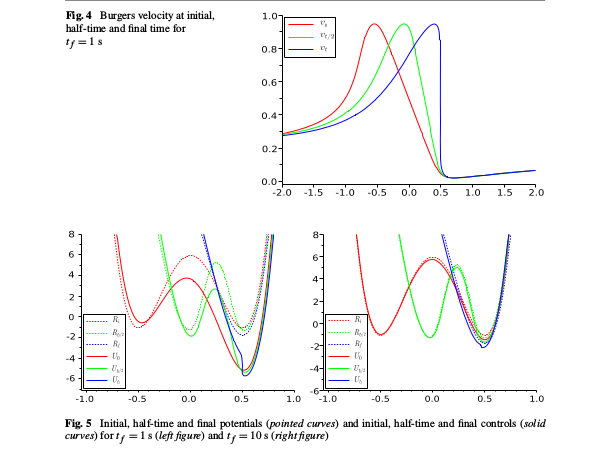
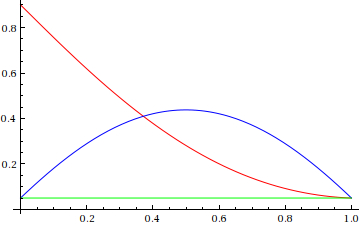
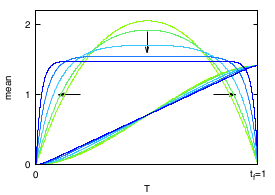
In a series of distinct collaborations, we proved that thermodynamic transitions in non-equilibrium thermodynamics described by Markov processes (overdamped, underdamped with arbitrary or kinetic plus potential Hamiltonian, pure jump ) always occur with average entropy production
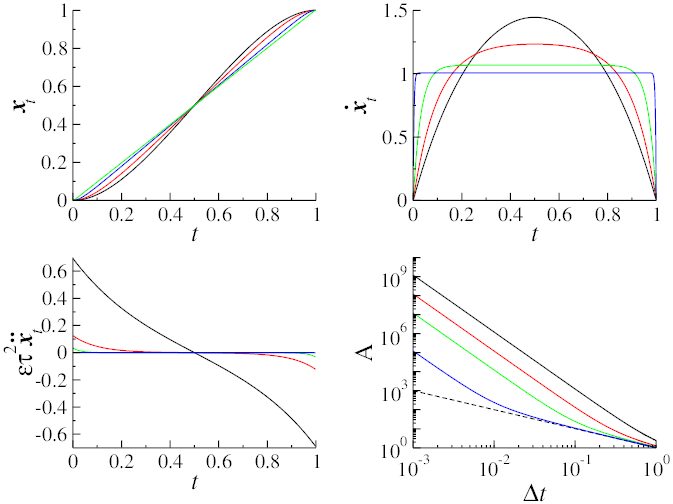
bounded away from zero. Optimal control problems are notoriously sensitive to the class of admissible protocols. In all the cases above, optimal protocol are smooth and non-equilibrium: the current velocity at the end of the control horizon is non-vanishing.
We also succeeded to develop a systematic analytic theory to compute underdamped corrections to overdamped Schrödinger bridges.