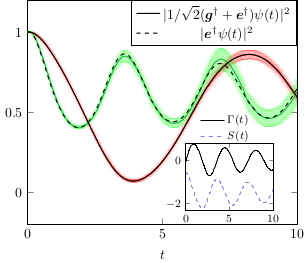
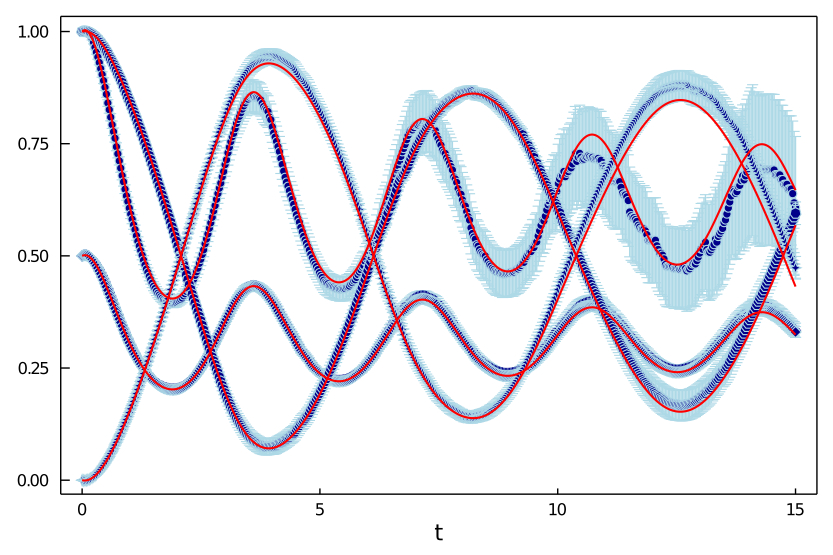
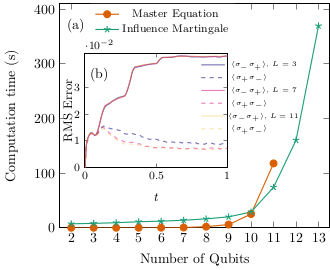
$$ \boldsymbol{\rho}_{t} = \operatorname{E} \Big{(}\mu_{t}\boldsymbol{\psi}_{t}\boldsymbol{\psi}_{t}^{\dagger}\Big{)} $$ We proved that the most general quantum master equation, the completely bounded master equation, may be solved by averaging over the realizations of a Markov process in the Hilbert state of the open quantum system. We later further developed the theory to prove the existence of a duality at the level of unraveling between completely positive and completely bounded master equations. These results have interesting applications to quantum error mitigation. An efficient numerical implementation of the influence martingale is now available in QuTip v5 as `nm_solve'. The tutorial is in github.