Results
Some results I have contributed to.
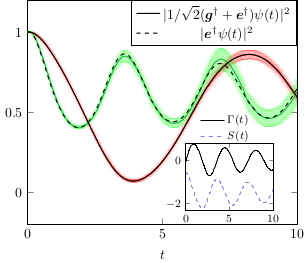
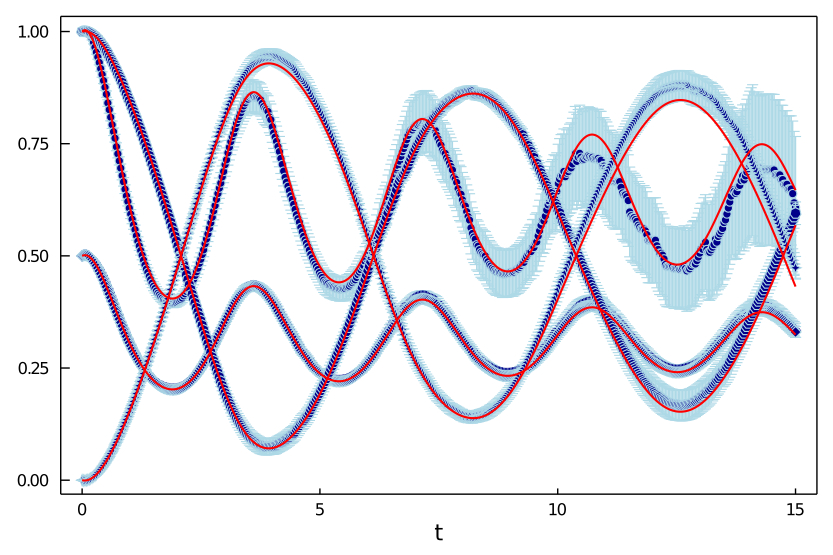
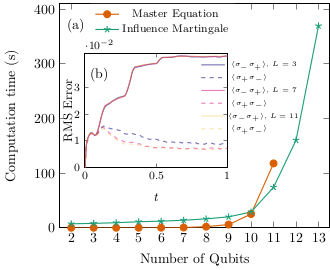
Unraveling of Completely Bounded Dynamical Maps
1 / 3
2 / 3
3 / 3
$$ \boldsymbol{\rho}_{t} = \operatorname{E} \Big{(}\mu_{t}\boldsymbol{\psi}_{t}\boldsymbol{\psi}_{t}^{\dagger}\Big{)} $$
We proved that the most general quantum master equation, the completely bounded master equation, may be solved by averaging over the realizations of a Markov process in the Hilbert state of the open quantum system. We later further developed the theory to prove the existence of a duality at the level of unraveling between completely positive and completely bounded master equations. These results have interesting applications to quantum error mitigation. An efficient numerical implementation of the influence martingale is now available in QuTip v5 as `nm_solve'. The tutorial is in github.
Refined Second Law for Markov Processes
1 / 5
2 / 5
3 / 5
4 / 5
5 / 5
6 / 5
$$ E\,\geq\,\mathrm{K_{B}}\,T\,\ln 2 $$
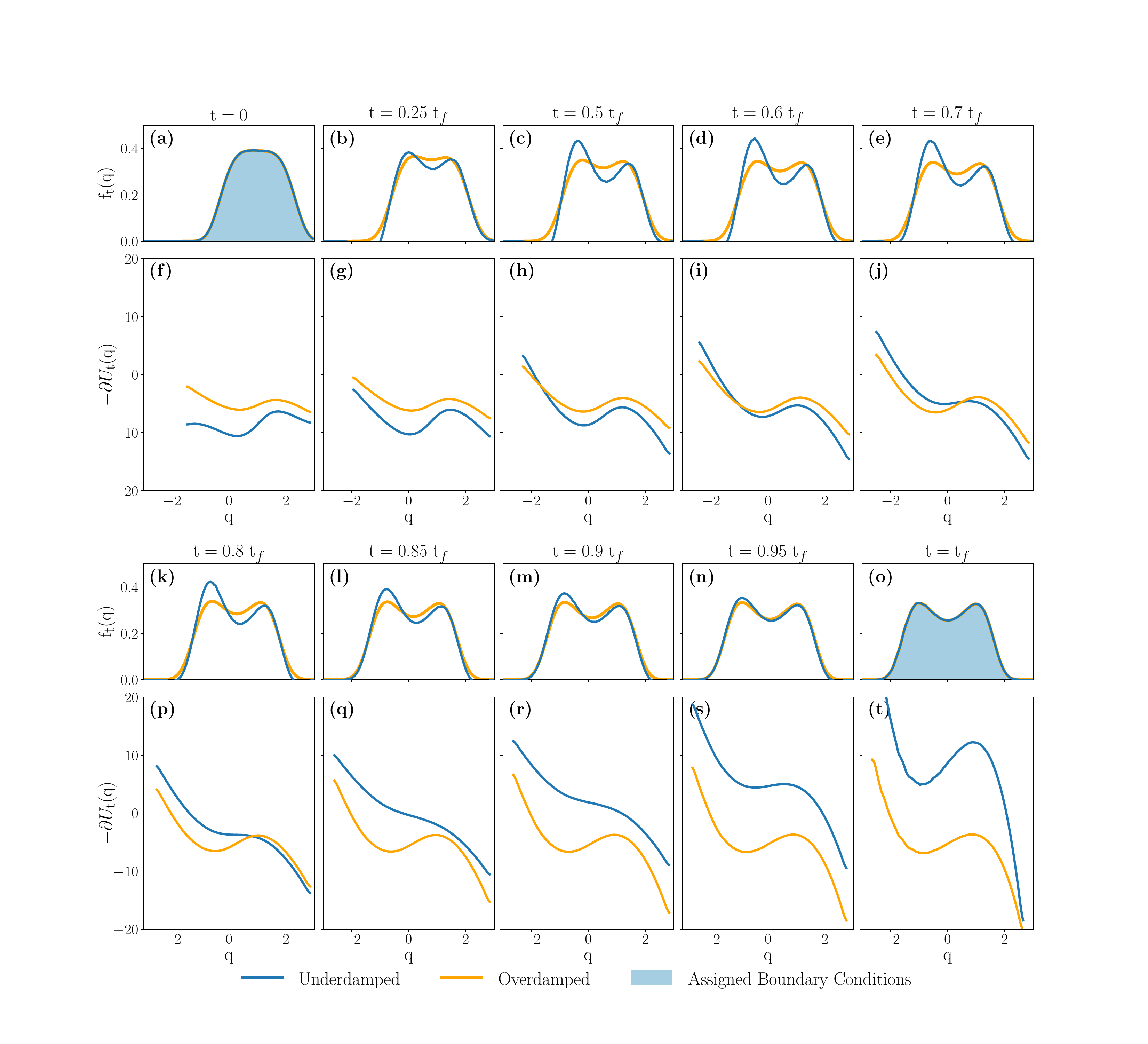
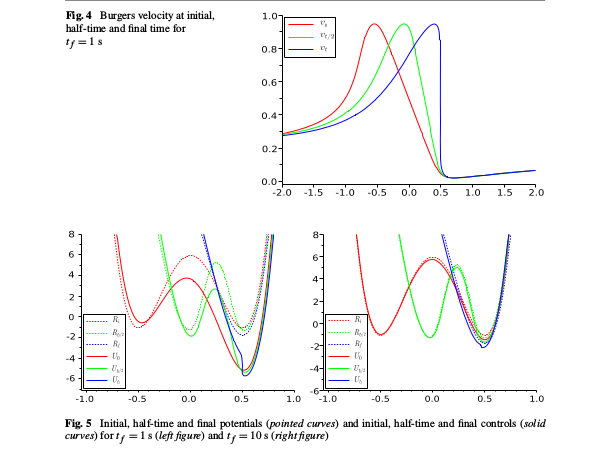
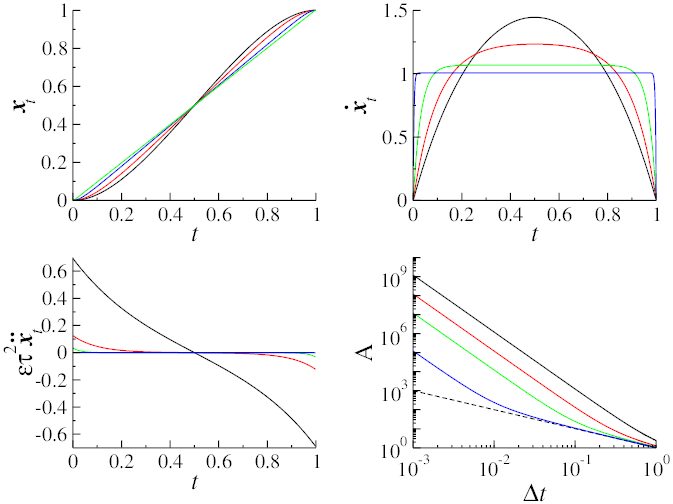
In a series of distinct collaborations, we proved that thermodynamic transitions in non-equilibrium thermodynamics described by Markov processes (overdamped, underdamped with arbitrary or kinetic plus potential Hamiltonian, pure jump ) always occur with average entropy production
bounded away from zero. Optimal control problems are notoriously sensitive to the class of admissible protocols. In all the cases above, optimal protocol are smooth and non-equilibrium: the current velocity at the end of the control horizon is non-vanishing.
We also succeeded to develop a systematic analytic theory to compute underdamped corrections to overdamped Schrödinger bridges.
It is also possible to impose constraints (via valley method or via an upper bound ) on the protocols' acceleration. This is in my view a realistic way to inquire speed way to address speed limits and shortcuts to equilibration of therodynamic transitions.
Multiscaling in the Kraichnan Model of Passive Advection
$$ \mathcal{S}_{2\,n}(\boldsymbol{x};m)=\operatorname{E}|\theta(\boldsymbol{x};m)-\theta(\boldsymbol{0};m)|^{2\,n}\propto \|\boldsymbol{x}\|^{\zeta_{2\,n}(\xi)} $$
Kraichnan's model of passive advection is to-date the only PDE model of turbulence where intermittency and multiscaling can be proven in a mathematically controlled fashion. The result was first independently derived in the diffusion , large dimension , and laminar limits and numerically also by us here.
The connection between multiscaling and intermittency is due to the existence of statistical conservation laws, martingales, associated to shapes formed by Lagrangian particles in their many body translational invariant configuration space.
In retrospective, the result of Kupiainen et al. I am most pleased with, is having clarified the relation between quantum field theory methods and scaling predictions based on many body Hopf's equations.
Later here and here , I used these methods to exhibit how a geometric signature is encoded in the scaling exponent as their perturative expressions admits a classification in terms of Gel'fand-Zeitlin patterns of \(\mathrm{SL}(N\,,\mathbb{R})\) in agreement to an early general conjecture.
In retrospective, the result of Kupiainen et al. I am most pleased with, is having clarified the relation between quantum field theory methods and scaling predictions based on many body Hopf's equations.
Later here and here , I used these methods to exhibit how a geometric signature is encoded in the scaling exponent as their perturative expressions admits a classification in terms of Gel'fand-Zeitlin patterns of \(\mathrm{SL}(N\,,\mathbb{R})\) in agreement to an early general conjecture.
Functional Determinants in the Stationary Action Approximation
$$ \frac{\mathrm{Det}O_{\mathcal{A},t_{\mathfrak{0}},\mathfrak{t_{1}}}^{(u_{\mathfrak{1}})} }{\mathrm{Det}O_{\mathcal{A},t_{\mathfrak{0}},\mathfrak{t_{1}}}^{(u_{\mathfrak{1}})}}=\frac{\mathrm{det}(A_{\mathfrak{0}}+A_{\mathfrak{1}}\Phi_{*\, t_{\mathfrak{0}},\mathfrak{t_{1}}}^{(u_{\mathfrak{1}})})}{\mathrm{det}(A_{\mathfrak{0}}+A_{\mathfrak{1}}\Phi_{*\, t_{\mathfrak{0}},\mathfrak{t_{1}}}^{(u_{\mathfrak{1}})})} $$
A beautiful result by Robin Forman yields a powerful expression of functional determinants occurring in elliptic boundary value problems.
Functional determinants occurring in the stationary action approximation in finite dimensional Quantum Mechansics and non-equilibrium Statistical Mechanics
admit an explicit expression for any elliptic boundary conditions.
In my Physics Report , I used Forman's result to present a new derivation of Gutzwiller's trace formula. In my view functional determinant theory offers a particularly appealing way to understand topological invariance of Masolv and Conley and Zehnder indices in periodic orbit theory.
In my Physics Report , I used Forman's result to present a new derivation of Gutzwiller's trace formula. In my view functional determinant theory offers a particularly appealing way to understand topological invariance of Masolv and Conley and Zehnder indices in periodic orbit theory.
The Concept of "Strong Anomalous Diffusion"
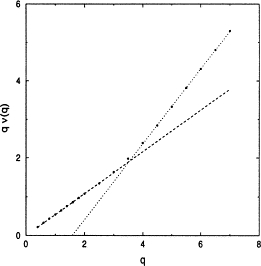
$$ \operatorname{E}|\xi_{t}-\operatorname{E}\xi_{t}|^{q}\propto t^{q\,\nu(q)} $$
In Castiglione et al (1999) we inquired the mechanisms
underlying genuine multiscaling in diffusion processes. Strong anomalous diffusion appears in fine-tuned parametric regions of chaotic dynamical systems.
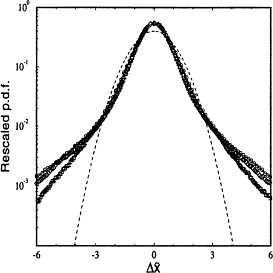
In such regions the interplay between self-similar bulk behavior of the statistics and ballistic transport for the rare excursions occasions non-linear corrections \( \nu(q) \) (typically "bifractal") to the diffusion scaling exponents.
A grand theoretical challenge is the developmemt of an analytical theory to compute anomalous scaling exponents. This task can be accomplished only in special cases .